Optical and radiation pyrometers

Pyrometer is a device which uses the relationship between the electromagnetic radiation emitted by a body and the temperature of this body. In order to better understand the phenomenon which forms the basis of pyrometry, it is useful to explain the concept of the blackbody, and the differences between it and real objects.

The term blackbody is ideal, and designates a body which radiates more electromagnetic energy for all wavelengths intervals than any other body of the same area and at the same temperature, and absorbs all the radiation it intercepts. Fig.1 presents one of the classical blackbody model.

Figure 1. A classical blackbody model.

The temperature of the blackbody determines the nature and extent of such radiation. Stefan-Boltzmann’s law says, that

the blackbody with a finite absolute temperature (T) emits radiant (ie, in all directions) electromagnetic radiation (EMR) per unit area of this blackbody and per second with intensity which is proportional to T⁴, according to an equation:

                                     E_T = σ * T⁴,                                                     (2)

where,

E_T - total EM energy emitted by the blackbody in all directions per unit area (1.m²) and per unit time (1,s),W/m²;

σ  - Stefan-Boltzmann’s constant, equal to 5.67051*10^-8, W/(m²*K⁴);

T  - an absolute temperature of the blackbody, K.

Fig. 2 shows the relationship between EMR emitted by a perfect blackbody as a function of temperature. The area under these curves is equal to the total energy (emitted by a black body) per second per unit area. This body at low temperatures emits EMR in the region of long wavelengths. This region spreads from far-infrared to microwave region (5 mm < λ < 100 mm, where λ  is the wavelength in mm, 10^-6 m). With increasing the blackbody temperature, the emission peaks move into the region of shorter wavelengths. At very high temperatures the blackbody emits in the near visible wavelengths region. Visible region corresponds to the wavelengths from 0.7 mm (red) through 0.62 mm (orange), 0.58 mm (yellow), 0.53 mm (green), 0.47 mm (blue) to 0.42 mm (violet).

Real objects emit and absorb less EMR than blackbodies, and this difference is dependent on the wavelength, so nonblackbodies can not exactly follow relationship shown in Fig. 2. For this purposes corrections should be used, otherwise, the apparent temperature will be lower that the actual temperature. Also, it is necessary to take into account the loss of emitted radiation when it passes through the media between the emitting body and a measuring instrument.

Figure 2. EM radiation emitted by the blackbody at various temperatures.

There are two types of pyrometers: optical (monochromatic or narrowband) and radiation (total radiation or broadband) pyrometers. The last devices originally were called radiation pyrometers, then radiation thermometers, and more recently infrared thermometers. However, the first their name (radiation pyrometers) is still widely used at present. These devices have high accuracy of ±0.01 °C as a standard instruments, and from ±0.5 to ±1% for industrial purposes.

a). Optical pyrometers, sometimes referred to as brightness thermometers, generally involve wavelengths only in the visible part of the spectrum. When the temperature of the body increases, so does the intensity at any particular wavelength. If two bodies have the same temperature, then intensities of those two objects are equal. 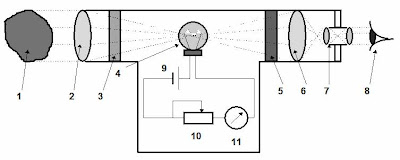In this type of a pyrometer the intensity of a certain wavelength of a heated body is compared with that of a heated platinum filament of a lamp (see Fig. 3 ).

Figure 3. An optical pyrometer.

An object 1 which temperature is to be measured, emits electromagnetic radiation with intensity proportional to its absolute temperature. This radiation passes through lens 2 and red optical filter 3. Optical filter picks out only the desired wavelength - red. Then radiation focuses on the platinum filament of a lamp 4, and passes through another filter 5, lens 6, viewing system 7. The viewer 8 sees the platinum filament superimposed on an image of the object 1. When the temperature of the filament is low comparing with that of the object, the viewer sees the filament as a dark line on the bright background image of the object. The lamp 4 is connected in series with an electrical battery 9, a variable resistor 10 and an ampermeter 11. By reducing the resistance of the resistor an electrical current passing through the filament increases. So does the temperature of the filament and its brightness. For a certain value of an electrical current (corresponded to a certain value of an object temperature), the brightness of the platinum filament will match the brightness of the object 1. At this setting the viewer cannot distinguish between the image of the object and the filament. At this time the measurement of temperature is performed. The scale of the ampermeter is calibrated in the units of temperature.

The lower temperature limit for optical pyrometers is determined by the temperature at which objects become visible in red (about 225 °C). However, there are devices which are able to measure even lower temperatures down to -50 °C. The upper limit varies from 600 to 3000 °C, and is limited by the melting point of the platinum filament. An accuracy is typically varied from ±5 to ±10 K.

b). Radiation pyrometers, being very simple and cheap, use an exponential relationship between a total emitted EMR energy and given temperature. In radiation pyrometers (see Fig. 4) EMR energy emitted at infrared (2.5 < l < 20 mm) to visible wavelengths (0.42 < l < 0.7 mm) from an object 1 is focused by a spherical reflector 2 on a series of micro-thermocouples attached to a blackened platinum disc 3. The radiation is absorbed by the disc, which temperature is increased, so does thermal electromotive force U developed by the series of thermocouples. This thermal electromotive force is proportional to the temperature of hot junctions of thermocouples, and, finally, to the temperature of the object 1. The advantage of these pyrometers is that their operation slightly depends on the wavelength.

Figure 4. A total radiation pyrometer

The lower limits for radiation pyrometers vary from 0 to 600 °C, the upper limits vary from 1000 to 1900 °C. The accuracy varies from ±0.5 to ±5 K, depending on cost. They are widely used for temperature measurements in metal production facilities, glass industries, semiconductor processes, etc.

Article Source:: Dr. Alexander Badalyan, University of South Australia

Read more...

Thermistors Basics

If semiconductors or heat-treated metallic oxides (oxides of cobalt, copper, iron, tin, titanium, etc.) are used as the materials for producing temperature sensitive elements, then these temperature transducers are called thermistors (the name is derived from the term of ‘thermally sensitive resistor’). These oxides are compressed into the desired shape from the specially formulated powder. After that, the oxides are heat-treated to recrystallise them. As the result of this treatment the ceramic body becomes dense. The leadwires are then attached to this sensor for maintaining electrical contact.The following relationship applies to most thermistors:

                                        R_t = R₀*e^{B*(1/T - 1/T}₀⁾    (1)

where,

R_T0 - resistance of thermistor at reference temperature T_0, K, Ohm;
R_T  - resistance of thermistor at temperature  T, K, Ohm;
B    - constant over temperature range, depends on manufacturing process and construction characteristics, 1/K.

Fig. 3.15 shows relationship between temperature and resistance for a thermistor.Thermistors have negative thermal coefficient of electrical resistance. It means that when temperature increases the electrical resistance of thermistor decreases. They have greater resistance change (this is an advantage) compared with RTD in a given temperature range. For example, if we compare what change in resistance will be caused by variation of temperature in 1 °C for Platinum and Copper RTD  and for thermistor (see Fig. 2) in the temperature range from 273.15 to 423.15 K (ie, from 0 to 150 °C), we will obtain the following values:

• for platinum RTD                 - 0.38, Ohm / ̊C;
• for copper RTD                    - 0.04, Ohm / ̊C;
• for thermistor                       - 0.65, Ohm / ̊C;

Figure 2. Thermistor resistance vs temperature curve.

Wheatstone bridge and resistance measuring constant current circuits, similar to that used in the case of RTDs, are used for resistance measurement of thermistors. Despite their high sensitivity, thermistors have a worse accuracy and repeatability (this is the disadvantage) comparing with metallic RTDs. Since the resistance vs temperature function for thermistors is non-linear (although, some modern thermistors have a nearly linear relationship of temperature vs resistance), it is necessary to use prelinearisation circuits before interacting with related system instrumentation. In addition, due to the negative thermal coefficient of electrical resistance an inversion of the signal to positive form is required when interfacing with some analog or digital instrumentation. Therefore, thermistors are not widely used in process instrumentation field, at least at present. However, they have been well accepted in the food transportation industry, because they are small, portable and convenient. Another field of their growing application are heating and air-conditioning systems, where thermistors are used for checking the temperature in flow and return pipes.

All the discussed above instrumentation for temperature measurement refers to contact-type devices, because their sensitive elements are immersed in the measuring media. When dealing with temperatures above 1500 °C, contact-type temperature measuring devices are not applicable, because irreversible changes occur in metals which form their sensitive elements. It is possible to perform non-contact measurement of temperature by optoelectronic transducers.

Article Source:: Dr. Alexander Badalyan, University of South Australia

Read more...