Thermocouples : Basics

Seebeck in 1821 discovered that thermal electromotive force (t.e.m.f.) is generated in a closed circuit of two wires made of dissimilar metals if two junction are at different temperatures. One junction is inserted into a measuring media, and it is called a hot or measuring junction. Another one, called a cold or reference junction, is kept either at 0 °C or at ambient temperature and is connected to a measuring instrument (millivoltmeter). 

The electronic explanation of this phenomenon is as follows:

the density of conduction electrons in two dissimilar metals is different. So, in the case when metals are brought into contact (welded together), the free (or conduction) electrons will flow from the metal with high their density to the metal with low density of the conduction electrons. As the result of this drift, a potential difference is produced in the boundary between these two metals. This potential difference will stop the flow of electrons. Since the metals are different, so they will differently respond to temperature variations. In other words, the variation of temperature will change the density and velocities of free electrons in two metals differently. This will cause the change in the magnitude of the thermal electromotive force.

Figure 1: schematically shows a thermocouple and a measuring instrument.

Figure 1:      Thermocouple and measuring instrument.
1 - hot junction;              2 - metal A;                     3 - metal B;

4 - connection head;                 5 - extension wires;

6, 7 - positive and negative terminals, respectively, of a measuring instrument;

8 - measuring instrument.

T.e.m.f. is proportional to the difference of temperatures between the two junctions. All tables, correlated t.e.m.f. of thermocouple (measured in mV) and temperature, are developed when the temperature of a cold junction is equal to 0 °C. T.e.m.f. is the function of temperature difference between the hot and the cold junctions:

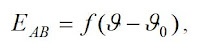                                       (1)

where:

E_AB               - t.e.m.f. developed by a thermocouple, mV;

ϑ and ϑ₀        - temperatures of the hot and the cold junctions of a thermocouple, ̊C.

If the temperature of the cold junction is kept constant (say at 0, ̊C), then t.e.m.f. is proportional to the temperature of the hot junction (the measuring temperature), ie

                                               (2)

In reality, in industrial environment, however, it is not possible (or is not convenient) to keep the temperature of the cold junction at 0, ̊C. Therefore, to evaluate the actual t.e.m.f. and, finally, the actual measuring temperature, we should introduce a correction. A final equation has the following form:

                                                         (3)

where:

E_AB(ϑ,ϑ₀)       - t.e.m.f. developed by a thermocouple when the temperature of the hot  junction is equal to ϑ  and the temperature of the cold junction is equal to ϑ₀ = 0, ̊C ,mV;

E_AB(ϑ_,ϑ'₀)        - t.e.m.f. developed by a thermocouple when the temperature of the hot junction is equal to ϑ and the temperature of the cold junction is equal to ϑ'₀ (different from 0, ̊C) – this t.e.m.f. is measured by a millivoltmeter, mV;

E_AB(ϑ_0,ϑ'₀)      - t.e.m.f. developed by a thermocouple when the temperature of the hot junction is equal to ϑ'₀ and the temperature of the cold junction is equal to ϑ₀ = 0_, ̊C ,mV.

There are various types of thermocouples:

• Platinum and Platinum - 10% Rhodium (type S) from -50 to 1765 °C;

• Platinum - 6% Rhodium and Platinum - 30% Rhodium (type B) from 0 to 1820 °C;

• Nickel - Chromium and Nickel - Aluminium (Chromel-Alumel, type K) from -270 to 1370 °C;

• Iron and Copper - Nickel (Iron - Constantan, type J) from -210 to 1200 °C;

• Copper and Copper - Nickel (Copper - Constantan, type T) from -270 to 400 °C;

• Nickel - Chromium and Copper - Nickel (Chromel - Constantan, type E) from -270 to 1000 °C.

Figure 2 presents experimental curves thermal electromotive force vs temperature for several types of thermocouples.

Figure 2: Experimental curves thermal electromotive force vs temperature.

Requirements imposed to the properties of metals used as electrodes for thermocouples are as follows:

• reproducibility of material, ie possibility of obtaining of metal wires with the same properties;

• resistance of metal electrodes should be small and have a weak relationship vs temperature;

• stability of a static characteristic E_AB = f(ϑ), ie recovery of properties after measurements;

• high sensitivity;

• correlation E_AB = f(ϑ) should be close to linear relationship as much as possible.

The highest sensitivity has thermocouple of Type J (Iron - Constantan): S= 0.055, mV/°C.

Article Source:: Dr. Alexander Badalyan, University of South Australia

Read more...