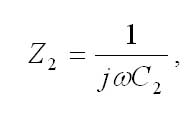The principle of these
pressure transducers is based on the well-known phenomenon, that when an
asymmetrical crystal is elastically deformed along its specific axes, an
electrical charge is developed on its sides. The value of this charge is
proportional to the force applied to the crystal, and, therefore, to the
pressure under measurement.
The principle of these
pressure transducers is based on the well-known phenomenon, that when an
asymmetrical crystal is elastically deformed along its specific axes, an
electrical charge is developed on its sides. The value of this charge is
proportional to the force applied to the crystal, and, therefore, to the
pressure under measurement.
Fig.
12
shows piezoelectric crystal circuit. An electrical charge developed on the
sides of the crystal is converted into a voltage-type signal using a capacitor.
This voltage is proportional to the electrical charge developed, and to the
pressure to be measured. Piezoelectric sensors cannot measure static pressures
for more than a few seconds, but they have a very quick response when measure
dynamic pressures.
Figure
12.
Piezoelectric pressure sensor with electrical circuit.
Synthetically developed
quartz crystals (barium titanate, lead zirconate) have similar properties as
natural single crystal (quartz). But natural quartz still is the perfect
material for manufacturing piezoelectric sensitive elements, because it has
perfect elasticity and stability, it is insensitive to temperature variations
and it has high insulation resistance.
These pressure transducers
are used for measurements of hydraulic and pneumatic pulsations, flow
instabilities, fuel injection, etc.
Let’s develop a differential
equation for this sensor.
 (60)
(60) 
.
(61)
The dynamic behaviour of a
piezoelectric element is analysed from mechanical and electrical points of
view.
,
(62), or using  (63)
(63)
we can get the following
second order differential equation:
(64)
or
(65)
Finally,
we can re-write (65) with variables in deviation form as follows:
(66)
Equation (66) is a second
order linear differential equation for a piezoelectric sensor with variables in
deviation form.
After
applying the Laplace transform to (66) we get a transfer function for the
piezoelectric sensor:
(67)
Ax - cross-sectional area of
the piezoelectric sensor in the direction
perpendicular to
axis ‘X’, m2;
b - charge sensitivity of the crystal to its
deformation in the direction
perpendicular to
axis ‘X’, C/m;
Fx - effective force due to
pressure in the direction of axis ‘X’, N;
k - stiffness of the crystal is large ≈ 2 x 109,
N/m;
Kx - steady state gain of the
crystal, in other words it is the charge sensitivity
of the crystal to
applied pressure , C/Pa;
m - mass of the crystal, kg;
qpiez - electrical charge developed
by the crystal, C;
P - pressure acting on the surface perpendicular
to axis ‘X’, Pa;
t - time, s ;
x - deformation of the crystal in the direction
of axis ’X’, m;
λ - constant (friction coefficient) for the
crystal, N*s / m .
Solution to equation (66)
will give us the variation of the electrical charge qpiez ,
developed on the surfaces of a piezoelement as a function of time for a step
change in the input variable – measured pressure, P . Now we should measure
this electrical charge. For this purpose two metal electrodes are attached to
the opposite sides of a piezoelectric crystal. Thus, a capacitor is formed. The
value of capacitance of this capacitor can be evaluated as follows:
 (68)
(68)
where,
Cpiez - electrical
capacitance of the piezoelement, F (Farad);
ε0 = 8.85, pF / m - the permittivity of vacuum, 1pF=10-12
F;
ε - the relative permittivity of the
material of the piezoelectric crystal,
this is the
dimensionless parameter;
Ax -
cross-sectional area of the piezoelectric sensor in the direction,
perpendicular to
the axis ‘X’, m2;
d - the thickness of the
piezoelectric crystal in the direction,
perpendicular to
the axis “X”, m.
The relative permittivity,
also called dielectric constant, for various piezoelectric materials is given
below :
· for quartz (natural
piezoelectric material) ε
= 4.5
· for tourmaline (natural
piezoelectric material) ε
= 6.6;
· for lead-zirconate-titanate
(man-made piezoelectric ceramic material) ε
= 1500;
· for lead metaniobate
(man-made piezoelectric ceramic material) ε
= 250.
It is also noted in the
above mentioned reference, that natural piezoelectric materials have very low
charge to force sensitivity, and therefore man-made piezoelectric ceramic
materials are used as sensing elements:
· charge sensitivity to force
for quartz 2.3,
pC/N;
· charge sensitivity to force
for tourmaline 1.9,
pC/N or 2.4, pC/N;
· charge sensitivity to force
for lead-zirconate-titanate 265,
pC/N;
· charge sensitivity to force
for lead metaniobate 80,
pC/N.
We need to develop an
electrical circuit which will allow us to convert variations of the capacitance
of the piezoelectric sensor into the variation of an easy measurable electrical
signal, voltage, for example. Such equivalent electrical circuit was developed,
and is named after Norton (see Figure 13)
Figure
13.
Norton equivalent electrical circuit for piezoelectric pressure/force
measurements. 1-
piezoelectric element, 2– connecting cable, 3– recorder.
The piezoelectric element
can be represented as a current source (or a charge generator) which is
connected in parallel with a capacitance Cpiez . Then, this element is connected to a voltage
recorder via connecting cables, which have the capacitance Ccable. A
recorder has a resistive load, Rload. The voltage measured across Rload
is equal:
 (69)
(69)
where, - the impedance of three resistances connected in parallel,Ohm
- the impedance of three resistances connected in parallel,Ohm
According to the definition,
the capacitance is equal to the ratio of the charge to the voltage across the
capacitor plates, according to:
 (70)
(70)
Let’s consider capacitance Cpiez:
 (71)
(71)
After
differentiating both sides of (71) we can get:
(72) or
 (73)
(73)
or, according to the Ohm’s
Law,
 (74)
(74)
Similar we can get
 (75)
(75)
Substitution
of (74) and (75) into (69) will give:
(76)
where, s = d/dt - the Laplace operator.
Expressing variables Vload and Ipiez in
deviation form and applying the Laplace transform to (76) we can get:
(77)
The transfer function for
the Norton equivalent electrical circuit for piezoelectric pressure/force
measurement system (see Figure 13)
is as follows:
(78)
According to the definition:
, (79). Expressing these variables in deviation form and
applying the Laplace transform to (79) we can get:
.
(80)
The transfer function
relating current and charge of the piezoelectric sensor is as follows:
.
(81)
The transfer function
relating the voltage Vload and the measured pressure P can be
determined as follows:
. (82)
After
substitution of (67), (78) and (80) into (82) we can get an expression for an
overall transfer function of the piezoelectric pressure/force measurement
system:
Article Source:: Dr. Alexander Badalyan, University of South Australia